IC-Design (3): Bandabstandsreferenz

Einführung
Bandabstandsreferenz, bei dem Wort knirschen meine Zähne, auf Englisch „bandgap voltage reference“ hört sich doch schon viel besser an 😀
Heute haben wir einiges vor, erstmal sorry für das Bild, aber ich hatte Probleme mit den Stiften und war wie immer zu faul für eine Korrektur :D.

Im erstem Teil werden wir uns mit dem PTAT current generator (a) befassen. Im Erstem Blogeintrag, haben wir die Spannungen für die einzelnen Stränge hergeleitet. Mit idealer (Temperaturabhängiger Spannungsquelle), können wir folgendes erwarten:

$\boxed{V_{BE1}= V_T*ln(\frac{I_D}{I_S}) (NTC)}$

$\boxed{V_{BE2}= V_T*ln(\frac{I_D}{I_S}) (NTC)}$

$\boxed{\Delta V_{BE}= R_1*I_D (PTC)}$

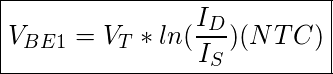
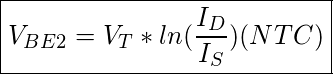
Für die Speisung der Stränge benutzen wir spannungsgesteuerte Stromquellen. Diese bekommen als Input die Spannung $V_X$ und regeln nach diesem den Ausgangsstrom. Ziel ist es den Widerstandswert $R_1$ zu finden, um den in Eintrag (2) bestimmten Strom $I_0 = 10\mu A$ einzustellen. Als Referenz gilt die Beziehung : $R = \frac{\Delta V_{BE}} {I_D}$ .

Das Bild zeigt den Schaltplan für den PTAT. Auf der linken Seite ist ein Startup-Circuit realisiert. Dieser dient dazu, die Schaltung zu starten, wenn die Spannungen an allen Punkten 0 sind. In diesem Fall würden die Eingänge der G0 und G2 nämlich das gleiche Potential besitzten. Deshalb gibt der Startup-circuit einen Strom in die Schaltung und sobald sie funktioniert, fließt kein Strom mehr über V1. Die Spannungsquelle V1 ist nur zur Messung des Stromes dort.

Zuerst stellen wir den Widerstandswert ungefähr ein. Aus dem zweitem Blogeintrag, bekamen wir die Kurve von $\Delta V_{BE}$ , welche sich zwischen 54mV-56mV bewegte. Für den Strom von 10 $\mu A$ ergibt sich ein Widerstand von 5.4-5.6kOhm.

Die Simulationsergebnisse zeigen den Strome $I_B$ :
-in Abhängigkeit von $R_{ideal}$ (links oben),
-in Abhängigkeit von $R_{real}$ (links unten),
-in Abhängigkeit von T ( $R_{ideal}, R_{real}$ auf 10 $\mu A$ eingestellt) (rechts oben).

Mit der Sheetresistance von $L/W = 1k\Omega / \mu m$ entspricht 5.56 $\mu m$ = 5.56kOhm. Somit ergibt sich:
$R_{real} = 5.56k\Omega$ , $R_{ideal} = 5.4k\Omega$

Für die Spannung $\Delta V_{BE}$ können wir sehen, dass sie mit steigender Temperatur, ebenfalls zunimmt. Das heißt, dass der Widerstand $R_0$ einen größeren Temperaturkoeffizienten hat als die beiden BJT’s?
Für den idealen Widerstand weißt die Spannung $\Delta V_{BE}$ eine geringere Steigung über die Temperatur auf, als der reale Widerstand. Beide Kurven schneiden sich bei ca $10\mu A$ , was 27°C und unserem Arbeitspunkt entspricht.
Für den realen Widerstand beträgt die Steigung 38.71nV/K

Bandgap Voltage reference

Durch den vorherigen Versuch, konnte die Temperaturabhängigkeit des BJT’s für den eingestellen Arbeitspunkt von $10\mu A$ ermittelt werden. Da später angepasst werden muss, vereinfache ich das ganze und sage der Widerstand verändert sich Bereich von 0°C-100°C mit einem Wert von $5.4k\Omega - 5.6k\Omega$ .
Das entspricht 200 $\Omega$ . Aus einem vorherigem Beitrag ist die Veränderung der Widerstände über die Temperatur bekannt. Der RNHR1000 wies Werte von $-4.554\Omega/K$ auf. Somit sollte der Widerstandswert R2 ca. bei $200/4.554 = 43.92k\Omega$ liegen.
Für die Simulation wurden ideale Stromquellen genutzt.
Im Schaltplan sind diese G2 und G0. Die linke Schaltung rund um G3, ist der Start-Up-Circuit, welcher gewährleistet, dass die Schaltung anläuft. Das Simulationsergebnis für den berechneten Widerstand von $43.92k\Omega$ ist folglich dargestellt:

Es ist klar zu sehen, dass die Kurve nicht der erwarteten entspricht. Sie hat einen fallenden Verlauf und der Temperaturkoeefizient ist in keinem Bereich 0.
Durch eine Anpassung des Widerstandes auf den Wert $46.38k\Omega$
erhalten wir eine Kurve, die bei 50 °C einen kompensierten Temperaturkoeffizienten aufweist. Somit sollte die Abweichung über den Temperaturbereich minimal sein. Die maximale Abweichung liegt bei 535.162 $\mu V$ über den gesamten Bereich.

Fractional-Bandgap
Als nächstes wird die Schaltung für den fractional-Bandgap simuliert. Diese wird eingesetzt, um eine beliebig geringere Spannung als die Eingangsspannung zu erzeugen. Ich habe mich für 600mV entschieden. Kurz gefasst wird die Spannung durch das Verhältnis aus R2/R3 angepasst. Mit dem vorher bestimmten Widerstandwert von $46.38k\Omega$ für R2 ergibt sich für R3 $23.19k\Omega$ . Wieder ist der Startup-Ciruit zu sehen, der wie wir gleich in der Simulation sehen werden noch nicht richtig funktioniert für diese geringe Spannung.Der Startup-Circuit fängt erst ab einer Temperatur von ca. 17°C an zu arbeiten. Außerdem liegt die Spannung auch nach dieser Temperatur nicht exakt bei 600mV.
Da die idealen Stromquellen und der OpAmp durch MosFets ersetzt werden, greife ich dieses Problem an späterer Stelle auf.

Was haben wir gelernt?
Die Arbeitspunkte rund um den 50×50 BJT wurden bestimmt. Der Widerstand R1 wurde für einen Strom von 10 $\mu$ ermittelt. Des weiteren die Widerstandswerte für R2&R3. Der Startup-Circuit hat noch Probleme bei geringeren Temperaturen und der Wert für R3 ist noch nicht perfekt eingestellt.
Was kommt als nächstes?
Im folgenden Beitrag werden die Eigenschaften der genutzten MOSFETs anhand von Simulationen bestimmt.