Ermittlung der BJT-Temperatur-Spannung


Aus dem vorherigem Artikel kennen wir die Spannung:
\boxed { \Delta V_{BE} = \eta * \V_t *log(n)},
welche unabhängig vom Bias-Strom I_B ist.
Nun wollen wir herausfinden, in welchem Bereich dies zutrifft. Dafür Simulieren wir die Spannung V_[BE} für verschiedene I_B, bei einer festen Temperatur (27°C). Wir sollten eine Kurve bekommen die ungefähr wie die in der Skizze aussieht. Für einen Punkt (sollte später möglichst in der Mitte des Temperaturbereichs liegen) ist der Temperturkoeffizient = 0.

Daraus können wir den Arbeitspunkt (für den Strom I_B) bestimmen. Wir wissen ja, dass der Strom sich ändern muss, damit wir für jede Temperatur die gleiche Ausgangsspannung erhalten.

Danach werden wir die konstante \eta bestimmen.
Zum Schluss wählen wir I_B nahe des rechten Rands (ja das hat er gesagt), simulieren \Delta V_{BE} für einen Temperaturbereich von 0 bis 100°C und bestimmen den Slope bei 27°C.


Im folgendem wurde \Delta V_{BE} für drei verschiedenen Transistorgrößen simuliert. 150×150, 100×100 und 50×50.

Zu erkennen ist, dass mit zunehmender Größer auch die Kurve abflacht. Der Arbeitspunkt für die einzelnen Transistoren ist wie folgt:

Rendered by QuickLaTeX.com



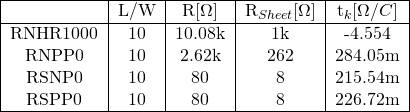
Nun berechnen wir die Konstante \eta aus der Formel für \Delta V_{BE} : \eta = \frac{ \Delta V_{BE} }{V_T *ln(8)}. Mit V_T = \frac{k*T(K)}{e} und T = (27°C)+273K ergibt sich für die jeweiligen Transistoren:
50×50: \Delta V_{BE} = 54mV :\eta= 2.313
100×100: \Delta V_{BE} = 54mV :\eta= 2.313
150×150: \Delta V_{BE} = 54mV :\eta= 2.313

Nun stellen wir unseren Arbeitpunkt mit I_B=10uA ein und plotten V_{BE1}, V_{BE2} und \Delta V_{BE} in einem Temperaturbereich von 0-100°C. Es ergeben sich folgende Grafiken aus den Simulationen:
\textbf{V_{BE1}, V_{BE2}, I_B=10\mu A, T=0...100°C}

\textbf{\Delta V_{BE}, I_B=10uA, T=0...100°C}

Da die Kurven linear sind, ist auch die Steigung/Slope zu jedem Zeitpunkt gleich. Für die Spannung \Delta V_{BE} ist diese bei allen Transistoren gleich und liegt bei 180.07\frac{\mu V}{°C}.
Im erstem Beitrag dieser IC-Design-Serie hatten wir eine Temperaturänderung von -2mV/°C an V_{BE1} = V_T*ln(\frac{I_D}{I_S}) und für V_{BE2} = V_{BE1} + V_T*ln(N). Für den anderen Temperaturkoeffizienten muss ich mich verbessern. Aufgrund der einfachhats haber habe ich ln(8) als 2 angenommen. Der Tempertaurkoeffizient ist natürlich 0.173mV/°C und nicht 0.167mV/°C . In folgender Tabelle sind die Simulationswerte für die Spannungen V_{BE1} und V_{BE2} dargestellt:
Rendered by QuickLaTeX.com

Charakterisierung der Widerstände

In jedem Prozess gibt es verschiedenste Arten von Widerständen aus denen für ds Design ausgewählt werden kann. Diese Unterscheiden sich in Ihren Eigenschaften, wie z.B. PTC- oder NTC-Verhalten oder der Sheet-Resistance(Widerstand pro Fläche W/L). Für meinen Prozess werde ich aus vier verschiedenen Widerständen wählen. Um die Eigenschaften der verschiedenen Widerstände zu ermitteln, setze ich eine Spannungsquelle mit 1V ein und messe die Veränderung des Stromes I_R durch eine Temperaturänderung.

Für die Weite wurden 1\mu m und für die Länge 10 \mu m gewählt.

Die Sheet-Resistance berechnet sich über den aktuellen Widerstandswert, multipliziert mit dem W/L-Verhältnis.
In der folgenden Grafik sind die Simulationsergebnisse dargestellt:

Da die Kennlinien nahe zu linear sind, kann der Temperaturkoeffizient einfach abgelesen werden. Diese Tabelle stellt die ermittelten Widerstands-Charakteristika übersichtlich da:

Rendered by QuickLaTeX.com

Was haben wir erreicht?
In diesem Beitrag wurden die einzelnen Transistoren und Ihre Temperaturabhängigkeiten bestimmt. Außerdem wurde ein Strom von 10\mu A als Arbeitspunkt gewählt, um eine stabile \Delta V_{BE} zu erhalten.
Für die verfügbaren Widerstände wurden ebenfalls die Temperaturabhängigkeiten sowie ihre Sheet-Resistance ermittelt.
Was kommt als nächstes?
Als nächstes werden wir den PTAT-current-generator, den normalen und den fractional Bandgap aufbauen um die ersten Arbeitspunkte einstellen. Einer davon wird sein, den Widerstand zu bestimmen, um einen 10\mu A Strom fließen zu lassen.