Hintergrund
Während meines Aufenthaltes im IIT Madras belge ich 3 Kurse. Neben dem RRAM und Electrical Vehicle and Renewable Energy Kurs, habe ich mich für IC Design and testing entschieden. Da wir viele Hausarbeiten haben und diese dokumentieren müssen, bietet es sich an, den geringen Mehraufwand in kauf zu nehmen und hier die verschiedenen Schritte darzustellen. In diesem erstem Post soll es um das grundlegende Verständnis des Schaltplans gehen.

Einführung

Darf ich vorstellen, eine temperaturunabhängige Konstant-spannungsquelle, die Bandgap-Schaltung. Für die späteren Beiträge werde ich den Fractional Bandgap benutzen, da ich diesen im Rahmen der Vorlesung designen werde.


Sieht erstmal ziemlich erschlagend aus, kann ich verstehen. Also erstmal 10 Schritte zurück.

Woher bekomme ich eine konstante Spannung?
Dafür schauen wir uns zuerst das Verhalten einer Diode an:


Der Strom fließt durch die Diode und ist abhängig von der angelegten Spannung. Die Formel ist in dem Bild gegeben. ist die angelegte Spannung und eine mit der Temperatur veränderliche weitere Spannung.
In der Skizze ist die Kennlinie des Stromes in Abhängigkeit der Spannung in blau gezeichnet. Der Strom steigt exponentiell bei Erhöhung der Spannung an. Zu Vereinfachung nehmen wir an, dass ab einer Spannung von ca. 0.7V eine Erhöhung der Spannung eine unendliche Änderung des Stromes zur Folge hat. Wenn wir also einen Strom speisen der Temperaturabhängig ist, ändert sich an der Spannung kaum etwas, wenn er immer in dem Bereich nach liegt. Wir haben somit eine konstante Spannungsquelle.

Für den BJT gilt dies genauso, nur das wir anstelle von den Strom und für die Spannung (NPN) und (PNP) haben.
Sieht bisher ziemlich einfach aus, an Schaltungsentwurf. Problem ist aber die Temperaturabhängigkeit der Diode.

Links im Bild sehen wir eine Konstantstromquelle die die Diode in unserem Arbeitpunkt betreibt. Die Spannung ergibt sich aus der vorherigen Formel für . In der Formel sind zwei Komponenten mit einer Temperaturabhängikeit. und . Die Pfeile sind nicht ganz korrekt, sowohl als auch steigten mit zunehmender Temperatur. Jedoch „gewinnt“ der und der logarithmus, wodurch die Spannung im Endeffekt bei höheren Temperaturen sinkt. Das Problem dabei ist, dass Werte von üblich sind. Bei einem Temperaturbereich von 100°C würden also -200mV Differenz in der Ausgangspannung auftreten 🙁

Hitman – Eliminierung der Temperaturabhängigkeit
Im vorherigem Abschnitt konnten wir die Temperaturabhängigkeit der bisherigen Diode charakterisieren. In der unteren Skizze ist diese unter 1 dargestellt. Wir haben einen positiven und negativen Temperaturparameter. Der positive (Vt) ist unabhängig von den Diodenparametern. Is hingegen ist von der Fläche der Diode abhängig. Mit steigender Flächer erhöht sich auch der Strom Is. Diesen Zusammenhang können wir uns zur nutze machen.

Erhöhen wir die Fläche um N fließt in dieser Diode nicht sondern . Wir erhalten neben dem ursprünglichen Term einen weiteren nur von Vt abhängigen.

Messen wir die Spannung zwischen zwei gleichen Dioden, wobei die eine die Fläche A und die andere N*A hat, so heben sich die “ -Terme“ auf. Es bleibt nur eine linear von Vt abhängige Spannung.

Diese Spannung besitzt eine Steigung , welche die gezeigte Charakteristik aufweist. Im folgendem wurde für N=8 gewählt, wodurch sich eine Steigung von ergibt.

Als nächstes werden genau diese beiden Dioden zusammengeschaltet, sodass wir in Summe die erhalten. Da der ursprüngliche Slope bei – beträgt, wird die Differenz der beiden Dioden um 12 verstärkt. Danach werden beide Slopes addiert, sodass wir letzten Endes eine Temperaturabhängigkeit von 0mV/K erhalten.


Und wie sieht jetzt die Schaltung aus?
Die Schaltung besteht neben den Dioden und den Konstatstromquellen aus einem Addierer, Multiplzierer und Differenzenbilder. Für all diese Funktionen kann ein Operationsverstärker genutzt werden. Das Problem sind in dieser Schaltung jedoch die geringen Spannungen. Jeder OpAmp kommt mit seinem eigenem Rauschen, Temperaturabhängigkeit und Fehlern (besonders der Differenzenverstärker aufgrund des Offsets). Es gilt also wie immer weniger ist mehr.
Einen Addierer tut genau das was der Name vermuten lässt, er addiert zwei oder mehr Spannungen. Der einfachste Weg zwei Spannungen zu addieren ist sie in Reihe zu schalten.

Die Skizze zeigt dies an und , welche sich addieren, wenn sie in Reihe geschaltet werden. Als ist die Diodenspannung (NTC-Verhalten) vorhanden. Es fehlt mit einem PTC Verhalten. Wieder wird der einfachste Weg gewählt, eine Spannung zu erzeugen, indem ein temperaturabhängiger Strom durch einen Widerstand geschickt wird. Dadurch fällt über dem Widerstand eine temperaturabhängige Spannung ab. Die Schaltung ganz rechts zeigt die Komponenten in Reihe verschaltet.

Als nächstes schalten schauen wir uns die bisherige Schaltung an (1). Sie besteht aus einer Diode die „parallel“ zu einem Widerstand mit Diode ist. Die Spannung zwischen den beiden Abgriffen in der Skizze soll ergeben.

Dafür muss an dem Widerstand also über den gesamten rechtem Strang anliegen. Um das zu bewerkstelligen, braucht es eine variable Stromquelle (2), die den Strom so lange verändert bis die gewollte Spannung anliegt. Als Stromquelle wird ein MOS-Transisor genutzt (3). Der fließende Strom kann durch eine Veränderung der Gate-Spannung beinflusst werden. Mit einer Erhöhung von verringert sich , bei einer Reduzierung von steigt .

Um eine automatische Einstellung zu bewerkstelligen benutzen wir einen OpAmp (4), der die Differenz zwischen den beiden Spannungen ermittelt und damit den Transistor aussteuert. Damit in beiden Dioden der gleiche Strom fließt wird der Mosfet eingesetzt, welcher zusammen mit einen Stromspiegel bildet. Nun fehlt noch der Multiplikator. Mit dem Widerstand , ergibt sich aus dem Verhältnis der Verstärkungsfaktor. Die Ausgangsspannung ergibt sich mit: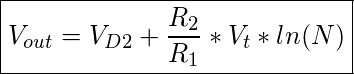

oder in den vorher bestimmten slopes .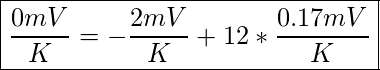  
Die Basic-Schaltung ist nun fertig. Es bleibt aber ein Problem, über die MOSFets, den Widerstand und die Diode fällt jeweils eine Spannung ab, sodass die Eingangsspannung >1.4V sein muss. Neben einer höheren Eingangsspannung die benötigt wird, müssen die Bauelemente auch für eine höhere Spannung ausgelegt werden, was besonders für kleine Technologien ein Problem darstellen kann. Noch anzumerken ist, dass die Ausgangsspannung Vout ist jedoch nur an einem Punkt nicht Temperaturabhängig. Dieser Punkt sollte möglichst in der Mitte des Temperaturbereichs gewählt werden.


Reduzierung der benötigten Versorgungsspannung
Zuvor haben wir die PTC und NTC Spannungen voneinander abgezogen, indem wir sie in Reihe geschaltet haben. Eine weitere Methode ist es, die Ströme aufzuteilen, durch eine parallel Schaltung. Wir haben die Spannung als „NTC“ Spannung oder auch CTAT gennant. Schalten wir zu der Diode einen Widerstand parallel, so ergibt sich der dort fließende Strom aus . Die über den Widerstand abfallende Spannung ist CTAT. Nun fließen nicht mehr die gleiche Ströme in und .

Indem wir den gleichen Widerstand parallel zu () schalten, ergibt sich der gleiche Strom durch beide Dioden. Der Strom durch und ergibt sich aus . So bildet sich der Strom ohne T-Koeffizient aus oder auch . Der Widerstand wird nicht mehr benötigt.

Als letztes schalten wir einen Widerstand zusammen mit einer Stromquelle parallel, so dass durch diesen der gleiche Strom fließt. Dieser ist Temperaturunabhängig und ist gegeben durch I_R4 = . Die Spannung über den Widerstand ergibt sich mit 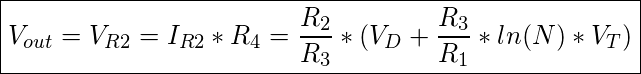. Durch den Widerstand kann also die Ausgangsspannung eingestellt werden.

Diese Schaltung wird als fractional Bandgap bezeichnet und ist diejenige, die in den folgenden Tutorials simuliert designed und gefertigt wird.

Wie geht es weiter?
Im nächstem Blog eintrag werde ich mit der Charakterisierung der BJT’s (anstelle der Dioden) sowie der benötigten Widerstände ansetzen. Die Simulationen werden mit Cadence Virtuoso durchgeführt.

Authors: Nassim Agrebi, Mohammad Habibur Reheman (iitm india)